
Ольга Давыдова
Педагог-психолог, историк, журналист, пишущий редактор
Математические принципы в окружающем мире. От морских раковин до спиралевидного расположения семян в подсолнечниках.
Золотое сечение восхищает умы учёных и художников на протяжении веков. Давайте точнее: тысячелетий. Число Фи, или примерно 1.618, описывает идеальные пропорции, которые можно обнаружить в самых разных формах жизни: от неживой природы до животного мира.
Первые известные применения Фи восходят к древним египтянам и грекам, хотя конкретное числовое значение, которое мы сегодня знаем как приблизительно 1.618, впервые было точно вычислено греческим математиком Евклидом в его труде «Начала» около 300 года до н.э. Евклид описал его как «деление отрезка на среднюю и крайнюю пропорцию», что является первой известной записью об использовании принципа золотого сечения.
В Средние века и эпоху Возрождения учёные и художники продолжили исследования, поскольку стремились к созданию произведений, гармонично сочетающих математику и красоту. Знаменитый итальянский математик Леонардо Пизанский, известный как Фибоначчи, внёс значительный вклад, показав, что последовательность Фибоначчи — последовательность чисел, в которой каждое последующее число является суммой двух предыдущих — асимптотически приближается к золотому сечению.
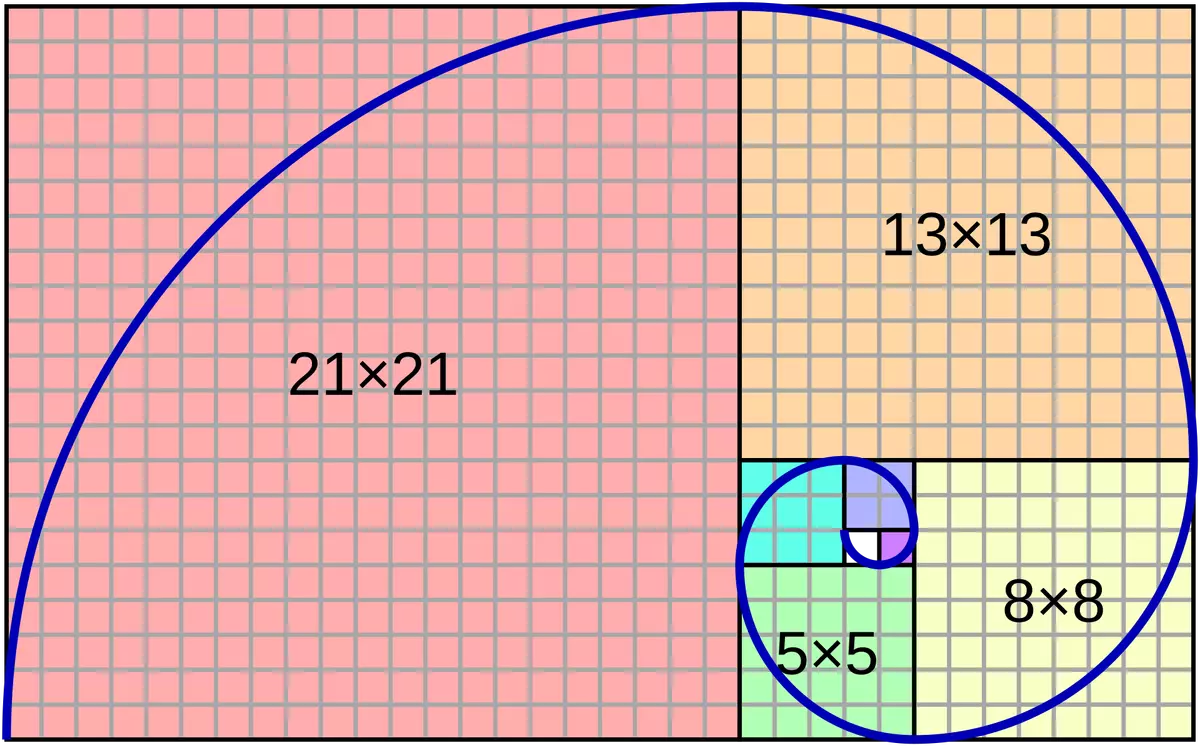
Спираль Фибоначчи: приближение золотой спирали, созданной путём рисования круговых дуг, соединяющих противоположные углы квадратов в мозаике Фибоначчи. Автор: Jahobr. Собственная работа, CC0
Источник: https://commons.wikimedia.org/w/index.php?curid=58460223
Почему «асимптотически»?
Термин описывает процесс или состояние, когда одна величина приближается к определённому значению, но никогда точно его не достигает.
В математике часто используется для описания поведения функций, которые приближаются к определённой кривой или линии (называемой асимптотой) по мере того, как переменная стремится к бесконечности или к определённой точке. Например, последовательность чисел, которая асимптотически приближается к золотому сечению, будет всё ближе и ближе к этому числу, но фактически никогда точно его не достигнет, хотя разница будет становиться практически незаметной.
В XV веке Лука Пачоли написал книгу «Божественная пропорция», которая подробно рассматривала золотое сечение. Его труды и иллюстрации, созданные Леонардо да Винчи для этой книги, сделали концепции золотого сечения имя среди архитекторов, художников, музыкантов и наконец биологов, открывших этот принцип в природных структурах и формах.
Взгляните на расположение листьев, цветов или семян в подсолнечнике. Каждое новое семя в центре подсолнечника располагается под углом, который оптимально минимизирует перекрытие с предыдущими, образуя спирали, которые раскрываются в обе стороны. Это не только красиво, но и позволяет растению максимально эффективно использовать доступное пространство и свет.
Или рассмотрите раковины моллюсков, например, наутилуса, где каждая новая камера раковины строится с увеличением предыдущей на коэффициент золотого сечения. Эта геометрическая прогрессия не только создаёт удивительно красивую спиральную структуру, но и обеспечивает равномерное распределение массы, что критически важно для подвижных морских существ.

Срез аммонита
Анатомия человека тоже не лишена этого феномена. Пропорции человеческого тела, расположение лица и рук часто следуют правилам золотого сечения, что, по мнению многих ученых, определяет восприятие красоты и гармонии в человеческой фигуре.
Что насчёт бо́льшего масштаба? Спиральные галактики во Вселенной также подчиняются этому принципу, где форма спиральных рукавов галактики может быть описана через золотое сечение.
Математические закономерности повторяются на всех уровнях природы. Кто-то всё ещё думает, что математика не пригодится в жизни?

Первые наблюдения фрактальных структур можно найти у математиков XIX века — Гастона Жюлиа и Пьера Фату, которые исследовали сложные итеративные процессы, формирующие визуальные паттерны, но истинную природу фракталов они понять не смогли.
Научное понимание пришло с работами Бенуа Мандельброта в середине XX века. Мандельброт, работавший в IBM, впервые вообще ввёл термин «фрактал» в 1975 году для описания повторяющихся комплексных структур, которые казались бесконечно самоподобными на всех уровнях масштабирования. Он продемонстрировал, как фракталы могут моделировать различные реальные феномены — от ценообразования на финансовых рынках до распределения галактик во Вселенной.
Множества Жюлиа и Мандельброта — это два особенных вида математических множеств, которые изучаются в контексте фрактальной геометрии.
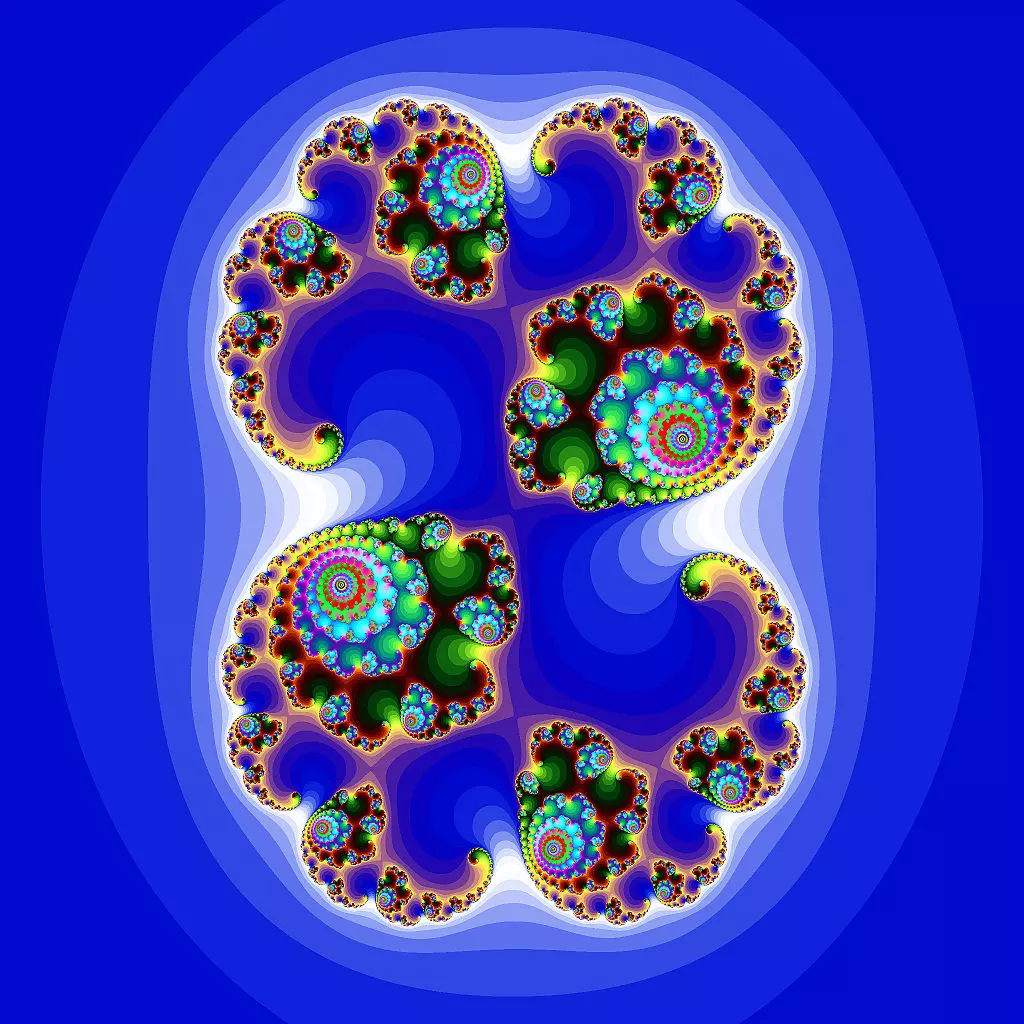
Множество Жюлиа. Авторство: Solkoll. Собственная работа, Общественное достояние
Источник: https://commons.wikimedia.org/w/index.php?curid=111840
Каждое множество Жюлиа создается с помощью специфической комплексной числовой формулы, при этом результат каждого последующего вычисления зависит от предыдущего. Это приводит к созданию уникальных, иногда бесконечно повторяющихся узоров. Можно сказать, что множества Жюлиа как будто исследуют, что происходит, если вы начинаете с определённой точки и применяете одну и ту же математическую операцию снова и снова.
Множество Мандельброта создаётся путем визуализации тех точек на комплексной плоскости, поведение которых остаётся «под контролем» при многократном применении одной и той же математической операции. Множество Мандельброта выглядит как узоры в форме бесконечно повторяющихся островов и побережий, и его часто называют «картой» для всех множеств Жюлиа, потому что каждая точка множества Мандельброта соответствует множеству Жюлиа с определенными свойствами.
С тех пор интерес к фракталам значительно вырос. Фрактальная геометрия предоставила новый способ описания сложных, нерегулярных форм и процессов в природе, от структуры облаков и рек до васкулярных и дыхательных систем.

Фракталы часто встречаются в ветвях деревьев и их корнях. Каждая большая ветка разветвляется на меньшие, которые, в свою очередь, повторяют этот процесс в уменьшенном масштабе. Так фрактальная структура обеспечивает оптимальное поглощение солнечного света и питательных веществ из почвы.

Река разветвляется на меньшие притоки, которые следуют аналогичному рисунку в более мелком масштабе. Здесь математика помогает максимизировать площадь дренажа в водосборном бассейне. Вода после дождя или от таяния снегов собирается реками и стекает в речную сеть, которая разветвляется по всему бассейну подобно веткам дерева. Эти «ветки» — маленькие ручьи и реки — позволяют воде собираться с большой площади и направляют её в одно большое русло или в озеро. Такой «дизайн» помогает использовать воду более эффективно, предотвращая затопления и обеспечивая равномерный сбор воды со всей территории.

Каждая снежинка уникальна, но обычно они имеют шестиугольную фрактальную структуру, которая повторяется на всех уровнях масштабирования. Эта геометрическая форма образуется при кристаллизации водяных молекул в условиях низкой температуры.
Почему у снежинок образуется именно такая форма?
Снежинки формируют шестиугольную структуру из-за молекулярной структуры воды, точнее из-за того, как водородные связи удерживают молекулы воды вместе при замерзании. В молекуле воды атом кислорода соединён с двумя атомами водорода под углом приблизительно в 104.5 градуса, что предопределяет образование шестиугольных структур при кристаллизации.
Когда температура падает и вода начинает замерзать, молекулы воды тяготеют к образованию наиболее стабильной конфигурации, которая минимизирует энергетические затраты, сохраняя при этом максимальную плотность. Водородные связи позволяют каждой молекуле воды соединяться с четырьмя другими, образуя шестиугольные сети, которые эффективно заполняют пространство и создают уникальные, но повторяющиеся геометрические формы снежинок.

Этот вид капусты славится своей четко выраженной фрактальной структурой. Каждый из его «бутонов» сам по себе представляет мини-копию всего кочана, повторяя форму спирали.

Кораллы создают фрактальные формы, которые помогают оптимизировать поглощение питательных веществ и света в водной среде. Эти сложные структуры предоставляют укрытие и пространство для множества морских видов, которые без рифов бы не выжили.

Листья многих видов папоротника демонстрируют классические фрактальные узоры с множеством повторений одного и того же формы листа в меньшем размере по мере приближения к краю.
Фрактальная структура листьев позволяет максимально увеличить площадь поверхности листа на ограниченном пространстве. Все ради эффективного фотосинтеза, так как большая площадь листа может поглощать больше солнечного света и улавливать больше углекислого газа.
Фрактальные узоры обеспечивают эффективное распределение воды и питательных веществ по всему листу. Ветвление жилок помогает равномерно транспортировать воду и минералы от стебля к краям листа.
И, наконец, фракталы делают растение устойчивее к физическим повреждениям. Если часть листа повреждена, фрактальная природа строения позволяет оставшейся части листа продолжать функционировать эффективно, минимизируя влияние повреждения.
Математические модели — особенно те, что основаны на природных паттернах и феноменах — это мощные инструменты для понимания и преобразования мира вокруг нас.

Математические модели помогают разобраться в сложных и, на первый взгляд, хаотичных системах. Например, понимание фрактальной природы распределения ветвей дерева или речных систем позволяет ученым предсказывать экологические изменения и разрабатывать стратегии управления природными ресурсами.
В метеорологии математические модели, основанные на фракталах, используются для прогнозирования погодных условий и климатических изменений. Например, помогают определить вероятность возникновения экстремальных погодных явлений, что критически важно, когда у вас не так-то много времени, чтобы подготовить город к стихийному бедствию.
В области материаловедения изучение природных структур — паутины или костей — привело к созданию новых, более легких и прочных материалов. Например, принципы фракталов применялись, чтобы создать более эффективные теплообменники и вентиляционные системы.
В биомедицине фрактальный анализ используется для изучения структуры и функций различных органов. Моделирование кровеносных сосудов, например, помогает создать методы лечения печально популярных сердечно-сосудистых заболеваний.
Архитекторы используют математические принципы для создания более функциональных и эстетически привлекательных пространств. Золотое сечение и фракталы — это база конструкций, которые гармонично вписываются в окружающую среду и оптимизированы с точки зрения использования ресурсов.
«Во-первых, это красиво». Художники и дизайнеры находят вдохновение в математических структурах, поскольку именно так создаются формы и конструкции, которые воспринимаются человеческим глазом и мозгом как визуально приятные и гармоничные.
В информационных технологиях алгоритмы, основанные на фрактальной математике, используются для сжатия изображений и видео, улучшения качества графики и оптимизации данных.


Педагог-психолог, историк, журналист, пишущий редактор
Понравился материал? Расскажите другим